— 反応速度定数 (HCN ↔ HNC) —
- 遷移状態理論 (アトキンス 27 章) の演習問題
演習問題
概要
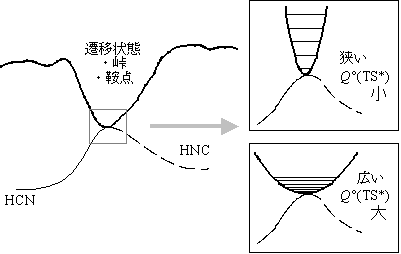
図 5-1. 遷移状態
「遷移状態」は原子核の位置を記述する多次元空間の中で、
反応物と生成物を結ぶ、最もエネルギーの低い経路に存在する障壁の位置
を指すものである。2次元平面で描けば、図 5-1 のように、2つの盆地
(反応物と生成物) の間にある、最も低い路にある「峠」である。
その形状は、馬につける鞍に似ていることから、ポテンシャル超曲面上の
「鞍点」と呼ばれることもある。
遷移状態理論による速度定数の式 (5-1) と 化学平衡定数の式
(4-1)
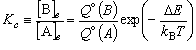 (4-1)
(4-1)
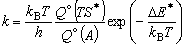 (5-1)
の類似性から、
「遷移状態理論は反応物と仮想的な遷移状態の間の平衡を仮定したもの」
と言われることも多い。しかし、これを別な角度から眺めると、
遷移状態の分配関数は、反応の経路に直交する座標に対する分子運動の
特徴を表現していると考えることが出来る。(図 5-1 右) すなわち、
遷移状態の分配関数の大きさは、経路の「広さ」を記述する量となっている。
(5-1)
の類似性から、
「遷移状態理論は反応物と仮想的な遷移状態の間の平衡を仮定したもの」
と言われることも多い。しかし、これを別な角度から眺めると、
遷移状態の分配関数は、反応の経路に直交する座標に対する分子運動の
特徴を表現していると考えることが出来る。(図 5-1 右) すなわち、
遷移状態の分配関数の大きさは、経路の「広さ」を記述する量となっている。
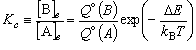 (4-1)
(4-1)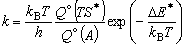 (5-1)
(5-1)
補足説明と演習のヒント
- 計算の手続きは、演習問題 4 とほぼ同様であるが、
遷移状態は非直線分子であるため、回転分配関数を評価する式は異なる (5-5)。
この演習の最後で、演習問題 4 の結果を用いるが、その値を示しておくと、
以下のようになる。
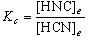 = 4.57
= 4.57  10−3 (@ 1000 K), 0.310 (@ 3000 K)
10−3 (@ 1000 K), 0.310 (@ 3000 K)