— 分子の回転状態分布 (HCl) —
- 統計熱力学 (アトキンス 19 章) / 分光学 (アトキンス 16 章) の演習問題
演習問題
演習問題 [3]概要
この例のような赤外吸収スペクトルは、
分子と、分子の置かれている状況に関する、以下のような情報を含んでいる。
横軸
演習問題を解くためには、 P(J), R(J)
と呼ばれる回転線の強度が、 回転量子数 J の状態の存在比 (濃度)
に比例することのみを理解すれば十分であるが、スペクトル線の現れる
波数の情報は、この分子に関する多くの情報を示している。
例えば、スペクトル線の間隔は、分子の回転定数を反映しているが、 この間隔が低波数側 (図 3-1 の右側) で大きくなっていることは、 振動励起状態 (
= 1) の分子の核間距離は、振動基底状態
(
= 0) の分子の核間距離よりも長くなっていることを示している。
また、各スペクトル線の分裂は 1H35Cl と
1H37Cl に起因するものであり、
同位体の振動波数の違いを反映している。
例えば、スペクトル線の間隔は、分子の回転定数を反映しているが、 この間隔が低波数側 (図 3-1 の右側) で大きくなっていることは、 振動励起状態 (
= 1) の分子の核間距離は、振動基底状態
(
= 0) の分子の核間距離よりも長くなっていることを示している。
また、各スペクトル線の分裂は 1H35Cl と
1H37Cl に起因するものであり、
同位体の振動波数の違いを反映している。
縦軸
この演習では主に縦軸の情報を利用する。各々の回転線の強度は
ほぼ、回転状態の分布 (濃度) を反映しているため、
ボルツマン分布を仮定すれば、分子の置かれた環境の温度を知ることができる。
この性質は、非接触型の温度計として温度計測にも利用されている。
(窒素分子のラマンスペクトルを利用することが多い)
振動スペクトルの回転構造
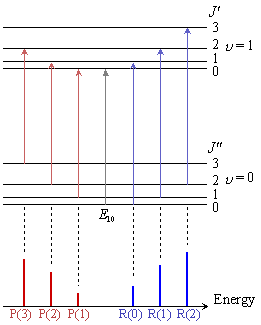
図 3-2. 振動スペクトルの回転構造
- 選択則
Δ
= ±1, ΔJ = ±1
- P 枝 (ΔJ = −1)
E[P(J)]
= E10 + B(J−1)J − BJ(J+1)
= E10 − 2BJ - R 枝 (ΔJ = +1)
E[R(J)]
= E10 + B(J+1)(J+2) − BJ(J+1)
= E10 + 2B(J + 1)
補足説明と演習のヒント
- ボルツマン分布則,
と回転エネルギー準位、多重度から導かれる関係 (3-5), (3-6) を用いて、温度 T を求める問題である。 実際の計算・プロットの際には、単位系の選択と換算を適切に 行うことが重要である。
,
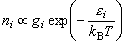- 分子の分光学定数は波数 [cm−1] (波長の逆数)
で与えられるのが一般的である。
これはエネルギーと線形な単位であるために、
事実上、エネルギーの単位としても頻繁に用いられる。
この演習で行うボルツマンプロットの横軸にも、多くの場合、
cm−1 がエネルギーの単位として用いられる。
- 1 [cm−1] = 100
c0 [Hz] = 100
c0
h [J]
- kB = 1.3807
10−23
/ (100
c0
h)
= 0.69504 [cm−1 K−1]
→
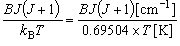
- 1 [cm−1] = 100