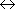 B の濃度平衡定数は、
B の濃度平衡定数は、
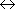 HNC)
HNC)
反応 A 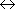 B の濃度平衡定数は、
B の濃度平衡定数は、
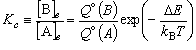 (1)
(1)
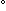 (A),
Q
(A),
Q 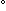 (B) は A, B の
(単位体積あたりの)
分配関数、
(B) は A, B の
(単位体積あたりの)
分配関数、 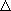 E
は反応のエネルギー差 (B の A を基準にしたエネルギー) である。
E
は反応のエネルギー差 (B の A を基準にしたエネルギー) である。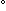 =
Q
=
Q  trans
Qelec Qvib Qrot
(2)
trans
Qelec Qvib Qrot
(2)
 trans,
Qelec, Qvib,
Qrot はそれぞれ、並進運動の (単位体積あたりの)
分配関数、 電子状態の分配関数、 振動分配関数、 回転分配関数である。
trans,
Qelec, Qvib,
Qrot はそれぞれ、並進運動の (単位体積あたりの)
分配関数、 電子状態の分配関数、 振動分配関数、 回転分配関数である。 HNC (3)
HNC (3)
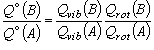 (4)
(4)
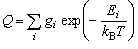 (gi : 状態 i の多重度,
Ei : 状態 i のエネルギー) (5)
(gi : 状態 i の多重度,
Ei : 状態 i のエネルギー) (5)
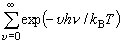 (6)
(6)
|
[問題 2(a )] (6) 式の和が等比級数であることから、 次式を導け。
|
m 個の振動自由度がある多原子分子では、 (6')
式を個々の振動の振動数  i
について計算して、 掛け合わせたものになる。
i
について計算して、 掛け合わせたものになる。
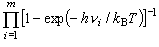 (7)
(7)
|
[問題 2(b )] HCN と HNC はいづれも4つの振動自由度を持ち、 振動の波数は HCN が 794, 794, 2177, 3286 (cm-1)、 HNC が 484, 484, 2062, 3655 (cm-1) である。 1000 K および 3000 K における、 振動分配関数の比 Qvib (HNC) / Qvib (HCN) を計算せよ。 次式を用いると計算が効率的になる。 |
直線分子は2次元の回転の自由度を持ち、 (5) 式の和を積分に置き換えることで、 次の式で近似できる。
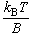 (B : 回転定数)
(8)
(B : 回転定数)
(8)
|
[問題 2(c )] HCN と HNC はいづれも直線分子であり、 その回転定数は、それぞれ 1.534 (HCN)、 1.555 (HNC) [cm-1] である。 回転分配関数の比 Qrot (HNC) / Qrot (HCN) を計算せよ。 HNC のエネルギーは HCN よりも、49.8 kJ mol-1 高い。 1000 K および 3000 K における、HCN と HNC の平衡定数、 KC = [HNC]e / [HCN]e を求めよ。 |