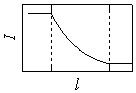
 |
| 図 1.1 ランベルト-ベール則 |
1.1 ランベルト-ベール則
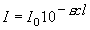 ,
,
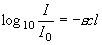 (1.1a)
(1.1a)
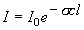 ,
,
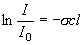 (1.1b)
(1.1b)
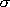 ,
,
 : 吸光係数 [次元: 濃度-1
長さ-1]
: 吸光係数 [次元: 濃度-1
長さ-1]
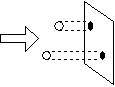 |
| 図 1.2 吸光断面積の古典的意味 |
[吸光係数]
 (底10): M-1
cm-1 (= dm3 mol-1 cm-1)
(底10): M-1
cm-1 (= dm3 mol-1 cm-1)
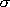 (底 e): (molecules
cm-3)-1 cm-1
= cm2 [molecule-1] 〜分子1個の影の面積
(底 e): (molecules
cm-3)-1 cm-1
= cm2 [molecule-1] 〜分子1個の影の面積
 = 5〜20 dm3 mol-1 cm-1) の UV
吸収スペクトルを測定したい。測定セルの光路長は 1 cm であり、
分光光度計の雑音などから透過率 90% 以上や 5% 以下の吸収は
精度よく測定できない。測定試料はどの程度の濃度に調整すればよいか?
= 5〜20 dm3 mol-1 cm-1) の UV
吸収スペクトルを測定したい。測定セルの光路長は 1 cm であり、
分光光度計の雑音などから透過率 90% 以上や 5% 以下の吸収は
精度よく測定できない。測定試料はどの程度の濃度に調整すればよいか?
1.2 波長領域と分子運動
[地球温暖化] 加熱=太陽光 (可視: peak〜500 nm) 冷却=地球放射 (赤外: peak〜10
冷却=地球放射 (赤外: peak〜10 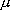 m)
大気は可視光に透明、赤外に分子吸収
m)
大気は可視光に透明、赤外に分子吸収 温室効果気体
温室効果気体[波長領域]
| 紫外 | 10〜380 nm | 電子遷移 |
| 可視 | 380〜780 nm | 〃 |
| 赤外 | 780 nm〜300  m m |
振動遷移〜回転遷移 |
| マイクロ波 | 300  m〜1 m m〜1 m |
回転遷移 |
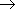 [Ne]3s03p1
[Ne]3s03p1 m)
m) 0 の遷移
0 の遷移 OH ラジカル生成源・オキシダント
OH ラジカル生成源・オキシダント注) GWP (Global Warming Potential / 温室効果ポテンシャル) は分子の赤外吸収によって主に決まるが、 放出された分子の大気中寿命にも依存する。
[波長-周波数/波数/エネルギー]
| 記号 | 単位 | |
| 波長 | 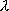 | nm,
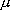 m (断らない限り真空中) m (断らない限り真空中) |
| 周波数 |  | s-1, Hz |
| 波数 | 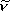 |
cm-1 |
| エネルギー |  ,
h ,
h | J (= J photon-1, or J molecule-1), kJ mol-1, cm-1 |
c0 : 真空中の光速 = 299792458 m s-1, NA : アボガドロ数 = 6.02213671023 mol-1
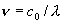 ,
,
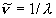 ,
,
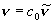
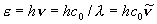 (1粒子あたり)
(1粒子あたり)
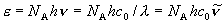 (1モルあたり)
(1モルあたり)
1.3 遷移の線幅
不均一幅:個々の分子の状態・環境の違いによる
均一幅 :状態の寿命などの性格による
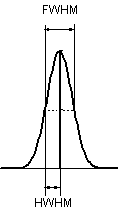 |
| 図 1.3 線幅 |
[ドップラー幅] (不均一幅)
−並進運動方向・速度が分子によって異なる(不均一)
 の光を発する分子が速度 s
で観測点から遠ざかる (+s) / 観測点に近づく(-s)
とき観測される周波数 (非相対論条件 s << c,
c : 光速)
の光を発する分子が速度 s
で観測点から遠ざかる (+s) / 観測点に近づく(-s)
とき観測される周波数 (非相対論条件 s << c,
c : 光速)
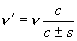 (1.2)
(1.2)
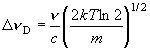 (1.3)
(1.3)
[寿命幅] (均一幅)
 で減衰
で減衰
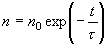 (1.4)
(1.4)
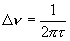 (1.5)
(1.5)
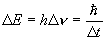 となり
Heisenberg の不確定性原理と一致
となり
Heisenberg の不確定性原理と一致
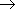 トンネル解離
トンネル解離 <自然幅>  自発発光寿命
自発発光寿命
<衝突幅, 圧力幅>  分子間衝突 /
分子間衝突 /
 = (衝突頻度)-1
= (衝突頻度)-1

 140
140  100
100  c0)
= 3.8
c0)
= 3.8  10-14 s = 38 fs (フェムト秒)
10-14 s = 38 fs (フェムト秒) 線 (121.534 nm)
のドップラー幅 (HWHM) は?
線 (121.534 nm)
のドップラー幅 (HWHM) は? 10-9)
10-9)
 [(2k
[(2k  298
298
 ln2) / (1.0087
ln2) / (1.0087  mu)]1/2 = 1.52
mu)]1/2 = 1.52  1010 s-1 (15.2 GHz) = 0.506 cm-1
1010 s-1 (15.2 GHz) = 0.506 cm-1 109 s-1 の頻度で空気中分子 (N2,
O2, etc.) と衝突する。これから衝突幅を見積り、
154.4 nm の電子遷移と 4.67
109 s-1 の頻度で空気中分子 (N2,
O2, etc.) と衝突する。これから衝突幅を見積り、
154.4 nm の電子遷移と 4.67  m の振動遷移について、
ドップラー幅と比較せよ。
m の振動遷移について、
ドップラー幅と比較せよ。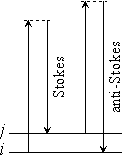 |
| 図 1.4 ラマン散乱 |
1.4 ラマン散乱
 I
と同じ周波数)
I
と同じ周波数)
 ij
だけシフト)
ij
だけシフト)
 scatter scatter |
=  I (レーリー散乱) I (レーリー散乱) |
=  I - I -
 ij (ラマン散乱,
ストークス光) ij (ラマン散乱,
ストークス光) | |
=  I + I +
 ij (ラマン散乱,
反ストークス光) ij (ラマン散乱,
反ストークス光) |
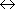 ラマン散乱:分極率による
ラマン散乱:分極率による[分極率]
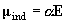 (1.6)
(1.6)